理解最大似然估计与最大后验估计
最大似然估计
最大似然估计(Maxiumum Likelihood Esimation, MLE)是频率学派对概率模型的一种参数估计方法。
它要解决的问题是,针对一定数量的独立重采样得到的样本,如何找到模型的参数 $\theta$,使得样本采样结果出现的概率最大。
具体来说,假设我们知道人身高的分布是正态分布,及概率密度函数的形式为:
其中,人身高的采样是独立同分布的,也就是你的身高不与别人的身高有关,且你们的身高服从同样的分布,即正态分布。
我们通过问卷调查,获得的一定数量人高的样本,然后估计身高分布模型的参数值方差 $\sigma$ 和均值 $\mu$。
似然函数
数学上采用似然函数来解释样本已知,而模型参数未知的情况。
似然函数 $f\left(x\left|\theta\right.\right)$ 指样本 $x$ 已知,而模型参数 $\theta$ 未知的函数。
假使模型的参数 $\theta$ 已知,而样本 $x$ 未知的函数 $f\left(\theta\left|x\right.\right)$ 为概率函数。
这有点像”一菜两吃“的意思,比如数学函数 $f(x,y)=x^y$,如果参数 $x$ 为定值,例如 $x=2$,则函数变为指数函数 $f(x,y)=2^y$;而如果 $y$ 为定值,例如 $y=2$,则函数变为二次函数。
因为似然函数的样本 $x$ 服从独立同分布,因此似然函数 $\begin{array}{l}f(x_1,x_2,…,x_n\left|\theta\right.)\end{array}$ 可以变为独立同分布的样本求联合概率:
求模型参数
例子
考虑这样一个例子,一个不透明的盒子里有黑白两种颜色的小球,有放回的进行100次抽取,记录下每次抽取小球的颜色,结果出现了80次黑色小球,20次白色小球,那么求盒子里的黑白两种颜色小球的分布情况?
转化为似然函数的问题,合理里其实黑白两种小球的分布已知,也就是说盒子中黑白小球的分布构成了模型,模型的参数已知,如何根据黑白球的采样情况,求盒子黑白球分布的情况。
我们假设黑球占比为 $p$,那么白球的占比就为 $1-p$,那么黑球每次被去取出的概率就等同于黑球的占比 $p$,因此,这次采样的似然函数为:
那么,模型的参数可以说有无穷种情况,如何计算模型的参数 $p$ 呢?
极大似然估计的思想就是,使当前采样情况出行概率最大的模型参数,为求得的结果,即使似然函数取得极大值。
因此要求得黑白球分布模型,即使似然函数取得极大值,也就是对似然函数求导,使导数为零,即为结果。很容易计算得到 $p=0.8$。
应用
其实我们日常生活中无意中就采用了极大似然估计的思想。
例子1
我们想进一步统计全国人民的身高分布的模型参数,虽然我们知道模型为某一种正态分布,但是我们无法对 14 多亿全国人民都逐一统计各自的身高。这时候,我们可以随机对各省的一部分人进行采样。因为这些省份各人间的身高为独立同分布的,所以可以基于这些样本,基于最大似然估计获得一个身高分布模型。该模型就可以近似的符合全国人民身高的分布模型。
频率派认为全国人民身高模型是一定的,就像柏拉图的理想型。通过不断的扩大样本的数量,就可以逼近这个背后真正的模型。
而贝叶斯派则认为模型本身也是不定的,这个模型初始有一个参数,可由先验知识获得,然后通过不断的采样修正我们的模型,使得最终的后验概率最大。
最大后验估计
最大后验估计是贝叶斯派的法宝,代表了另外一种看待世界的角度。
贝叶斯学派认为,对于要估计的模型人们会有一个预判,例如抛掷硬币正反硬币出现的次数应该五五开,这个预判就是先验函数 $p(\theta)$ 然后根据实际采样不断调整对这个模型参数进行调整,也就是说,这个模型参数本身是不能确定的,我们只能通过不断的实验逐渐获得最合理的模型参数,这一点就完全区别于频率学派的。
贝叶斯公式
最大后验估计的核心就是贝叶斯公式:
其中 $f(\theta\left|X\right.)$ 为后验概率, $p(\theta)$ 为先验估计,而 $f(X\left|\theta\right.)$ 为前面讲的似然函数, $p(X)$ 为边缘概率,可以简单的理解为一个归一化常数。
贝叶斯公式已经成为机器学习的核心算法之一,诸如拼写检查、语言翻译、海难搜救、生物医药、疾病诊断、邮件过滤、文本分类、侦破案件、工业生产等诸多方面都有很广泛的应用,它也是很多机器学习算法的基础。在这里,有必要了解一下贝叶斯公式。
贝叶斯公式是以英国学者托马斯·贝叶斯(Thomas Bayes)命名的。1763年Richard Price整理发表了贝叶斯的成果《An Essay towards solving a Problem in the Doctrine of Chances》,这才使贝叶斯公式展现在世人的面前。
贝叶斯公式是为了解决”逆概”;问题而提出的。正概问题很常见,比如不透明袋中有黑球M个,白球N个,随手抓起一个球,求是黑球的概率,大家心算一下就能知道是 $\frac{M}{M+N}$。当然,生活中有大量这样的例子,像人口流动统计、金融统计等等,这些统计的特征就是我们事先已经知道了所有样本的分布情况,在此基础上进行概率的计算,这就是“正概”问题。但是,如果我们不知道所有样本的信息(这样的例子比比皆是,例如物理学中我们不可能看到所有电子的运行状态,所以只能通过实验模拟观察大多数的情况去建立最合适的模型去解释),同时我们又想知道样本的概率怎么办呢?贝叶斯公式的作用就体现出来了。
还是一个袋子中装着若干小球,里面有黑色跟白色,我们随机取出一些小球,然后根据小球的情况去计算袋中小球实际的分布情况。此时我们可能有很多种模型(猜测)去解释,随着取出小球数量的增加,我们的模型也越来越精确,越来越逼近实际的情况,然后我们从这些模型中找出最贴合实际的。总结来说:不同模型的求解就是计算不同的后验概率(事件已经发生,求某种因素导致该事件发生的概率),对于连续的猜测空间是计算概率密度函数;模型比较如果不考虑先验概率(根据以往的经验和分析获得的概率)则运用了最大似然估计。这就是贝叶斯思想的核心。
下面我举一个例子:一所学校里面有 60% 的男生,40% 的女生。男生总是穿长裤,女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生,他(她)穿长裤的概率和穿裙子的概率是多大”,这个就是前面说的“正向概率”的计算。然而,假设你走在校园中,迎面走来一个穿长裤的学生(很不幸的是你高度近似,你只看得见他(她)穿的是否长裤,而无法确定他(她)的性别),你能够推断出他(她)是男生的概率是多大吗?
一些认知科学的研究表明(《决策与判断》以及《Rationality for Mortals》第12章:小孩也可以解决贝叶斯问题),我们对形式化的贝叶斯问题不擅长,但对于以频率形式呈现的等价问题却很擅长。在这里,我们不妨把问题重新叙述成:你在校园里面随机游走,遇到了 N 个穿长裤的人(仍然假设你无法直接观察到他们的性别),问这 N 个人里面有多少个女生多少个男生。
你说,这还不简单:算出学校里面有多少穿长裤的,然后在这些人里面再算出有多少女生,不就行了?
我们假设全校总共有H个学生,其中男生(都穿长裤)占60%,只有50%女生穿长裤。我们首先计算穿长裤的人数:H*P(Boy)*P(Pants|Boy)+H*P(Girl)*P(Pants|Girl),其中P(Boy)为男生比例,P(Pants|Boy)为男生中穿长裤的比率(此题中为100%),女生同理。其中创长裤的女生共有H*P(Girl)*P(Pants|Girl)个,两者一比,我们就得到:
式1
而这里面男生女生可以泛指一切事物,所以通用公式为:
—-(B’为B的互补,例如男生女生) 式2
其实分母就是指所有穿长裤的人的概率P(Pants)也就是P(A),分子是女生中穿长裤与是女生同时发生的概率,也就是P(Pants,Girl)或者说P(A,B),所以式2(全概率公式的一种特殊情况)又可以写为:
式3 又可以写为
式4
同理,我们可以得到P(A|B)*P(B)=P(A,B),所以:
P(A|B)*P(B) = P(B|A)*P(A),即:
式5
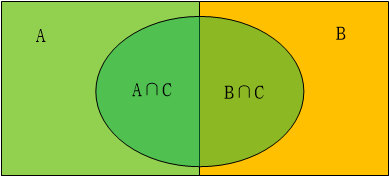
式3或式4也就是贝叶斯公式。其实式2是一个问题共有两种分类时的情况,例如性别、掷硬币等只有两种情况,现实生活中很多是由多种情况构成,一件事情可能由多个原因影响,那么推广开来,就是贝叶斯公式的通式。如图1-1所示,一个事物有两个影响要素A和B,面积的大小对应发生的概率大小,C事件的发生受到A和B要素的影响。如果计算在C事件发生是受到A事件影响的概率P(A|C),就是计算A∩C与C的面积之比,也就是P(A∩C)/P(C),P(A∩C)又可以写为P(A,C),因为P(C|A)表示A条件下C事件发生的概率,P(A)表示A事件发生的概率,即A的面积,所以P(A)*P(C|A)即A∩C的面积,也就是即A和C同时发生的概率P(A,C)。就得到P(A∩C)=P(A)*P(C|A), 同理:P(B∩C)=P(B)*P(C|B),因为得到 P(A|C)=P(A)*P(C|A)/(P(A)*P(C|A)+P(B)*P(C|B))。这是一个事物的影响因素由两个组成的情况,我们把所有情况统一起来就是全概率公式:
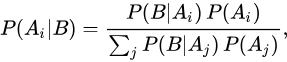
贝叶斯推断
什么是贝叶斯推断
贝叶斯推断(BAYESIAN INFERENCE)是一种应用于不确定性条件下的决策的统计方法。贝叶斯推断的显著特征是,为了得到一个统计结论能够利用先验信息和样本信息。
通俗来讲,我想知道A事件的发生,如果没有任何的先验知识,我只能做出它发生与不发生的概率各占50%的判断。但是,幸运的是我知道B事件发生了,根据两者的关联经验,我知道它对A事件的发生起到促进作用,所以我可以更加准确的判断A事件是大概率发生的(如80%),而不是起初的非零即一的50%。如果我有更多A的关联事件,那么我可以做出更加准确的判断,这就是贝叶斯推断。
我们还是看式5:$P(B|A)=\frac{P(A)*P(B|A)}{P(B)}$,P(A)是我们的先验概率,(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。$\frac{P(B|A)}{P(B)}$ 称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
为了更直观的解释贝叶斯推断,这里举一个维基百科的例子——吸毒监测:
假设一个常规的检测结果的敏感度与可靠度均为99%,即吸毒者每次检测呈阳性(+)的概率为99%。而不吸毒者每次检测呈阴性(-)的概率为99%。从检测结果的概率来看,检测结果是比较准确的,但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司对全体雇员进行吸毒检测,已知0.5%的雇员吸毒。请问每位检测结果呈阳性的雇员吸毒的概率有多高?
令“D”为雇员吸毒事件,“N”为雇员不吸毒事件,“+”为检测呈阳性事件。可得
- P(D)代表雇员吸毒的概率,不考虑其他情况,该值为0.005。因为公司的预先统计表明该公司的雇员中有0.5%的人吸食毒品,所以这个值就是D的先验概率。
- P(N)代表雇员不吸毒的概率,显然,该值为0.995,也就是1-P(D)。
- P(+|D)代表吸毒者阳性检出率,这是一个条件概率,由于阳性检测准确性是99%,因此该值为0.99。
- P(+|N)代表不吸毒者阳性检出率,也就是出错检测的概率,该值为0.01,因为对于不吸毒者,其检测为阴性的概率为99%,因此,其被误检测成阳性的概率为1 - 0.99 = 0.01。
- P(+)代表不考虑其他因素的影响的阳性检出率。该值为0.0149或者1.49%。我们可以通过全概率公式计算得到:此概率 = 吸毒者阳性检出率(0.5% x 99% = 0.495%)+ 不吸毒者阳性检出率(99.5% x 1% = 0.995%)。P(+)=0.0149是检测呈阳性的先验概率。用数学公式描述为:
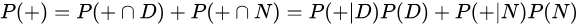
据上述描述,我们可以计算某人检测呈阳性时确实吸毒的条件概率P(D|+):
尽管吸毒检测的准确率高达99%,但贝叶斯定理告诉我们:如果某人检测呈阳性,其吸毒的概率只有大约33%,不吸毒的可能性比较大。假阳性高,则检测的结果不可靠。
同时,我们可以计算一下假如一个人吸毒,但他误检测成阴性的概率P(D|-):
$P(D|-)=\frac{P(-|D)P(D)}{P(-|D)P(D)+P(-|N)P(N)}$
=$\frac{0.01×0.005}{0.01×0.005+0.99×0.995}$
≈0.0000507
可见,一个人吸毒但被误检测为阴性的概率只有0.005%,也就是说一个人如果检测为阴性,则基本可以判定他没有吸毒。但是一个人如果监测为阳性,则只有33%的概率确定他吸毒。这在跟很多医学监测当中的案例很相似,假阳性比假阴性更值得我们关注!
贝叶斯推断与拼接纠正
贝叶斯推断其实有很多应用,例如语言翻译、中文分词、图像识别等,很多博客也以拼写纠正作为示例,这里我就详细讲一下拼写纠正的过程。
经典著作《人工智能:现代方法》的作者之一 Peter Norvig 曾经写过一篇介绍如何写一个拼写检查/纠正器的文章,详情戳这里。
用户在输入过程中,难免会遇到拼写错误的情况,我们要做的就是给出一个或几个纠正后的用户本来想要输入的单词推荐。这里的一个关键问题就是:用户到底想要输入什么单词?
其实用数学的语言来描述,就是要求出P(我们猜测用户要输入的单词|用户实际输入的单词)的大小。
用T表示我们猜测用户输入的单词,用S表示用户实际输入的单词,那么就是求P(t|S) = $\frac{P(S|t)×P(t)}{P(S)}$ 的大小。
对于同一个单词,P(S)的概率是一样的,那么就等价于P(t|S)∝ P(S|t)×P(t)。 ∝是正比于,不是无穷大
那么要是的P(t|S)最大,就是使得P(S|t)×P(t)最大。
P(S|t)名义上是指我们猜测的单词t是用户真正想输入单词的概率,不同的单词概率不同,这就涉及到最大似然估计。例如用户输入的单词是thriw,这时throw跟thraw都有可能,但是你会想到,o跟i很接近,用户可能要输的单词是throw的可能性比thraw的可能性大得多,根据最大似然估计找出最可能的单词。但是,有时候光有最大似然并不能完美的解决问题,我们还需要利用先验概率P(t)。
P(t)使我们猜测的单词出现的概率,这些单词t1、t2、t3….理论上有无穷种,但它是一种先验概率,对于单词来说,可能有点抽象。这里举一个分词的例子:
The girl saw the boy with a telescope.
如果仅用最大似然估计方法的话,可能会给出两种结果:1 The girl saw | the boy with a telescope 2.The girl saw the boy | with a telescope
但是根据我们的常识,一个女孩看着一个拿着望远镜的男孩?拿着望远镜有点莫名其妙,与“看”这个动作联系起来,那么最合适的解释恐怕是女孩拿着望远镜看那个男孩。那么得出这个结论,就是用到我们的先验知识,也就是P(t)。






